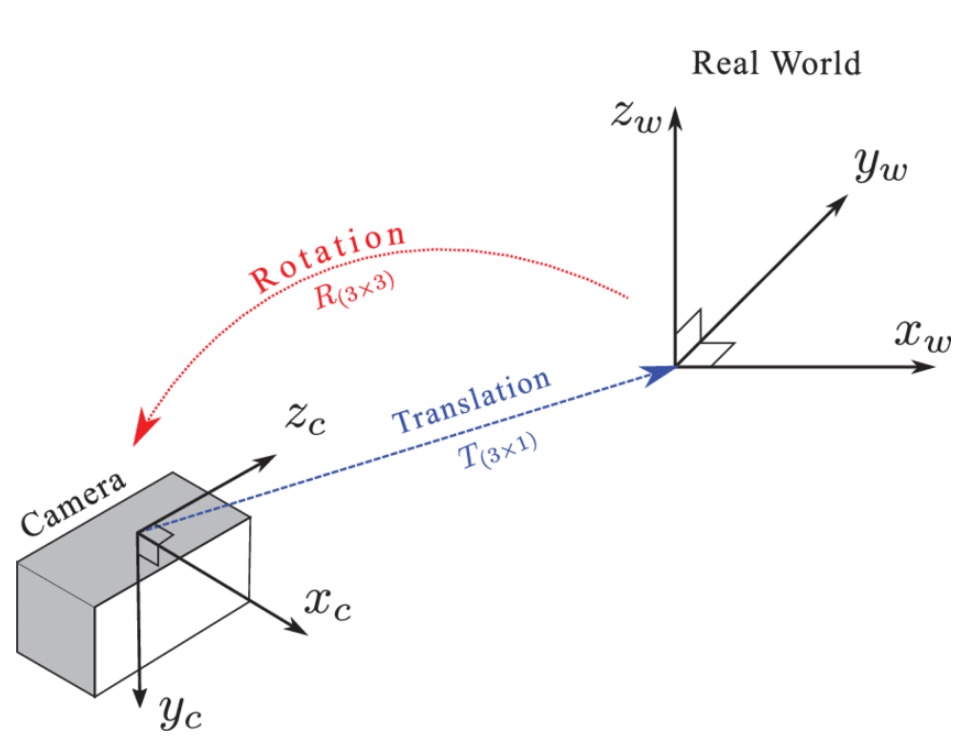
相机位姿, C2W, W2C

Camera pose

我们常说相机位姿用来相机的镜头朝向$R$+相机在世界坐标系空间位置$t$, 但是这个说法其实是有问题的，初学时容易陷入误区: “既然需要的是相机镜头的方向，为什么不使用三维的空间向量来表示，而是要使用四维的四元数” 这其实是表述时候引起的误解。所谓”相机镜头的方向”其实是不对的, 其实还隐含着相机的头顶朝向, 想象一下, 相机绕着镜头的中轴线旋转时, 此时镜头的方向都是相同的, 但是拍摄出的画面是完全不同的。

所以, 到底什么是相机的位姿?

首先, 位姿都是相对的概念, 必须有一个参考系我们才能谈论相机的位姿, “相机位姿(camera pose)”其实是一个省略的说法, 全程应该是”相机在世界坐标系中的位姿”。我们所处的世界空间就是我们常常默认而忽略的参考坐标系。

相机位姿的常见表示有$qvec+tvec$, 或者4×4的齐次$[R

t]$矩阵。下文中: $R$代表相机位姿的旋转矩阵, $t$代表相机相对于世界坐标系原点的位移向量, $T$代表4×4的变换矩阵$[R

t]$。

Q: 相机的位姿由旋转和位移组成，位移是相机在世界坐标系下的位置，旋转$R$又能代表什么？有什么物理含义？

相机位姿与”W2C, C2W”的关系

C2W

C2W(Camera to World)就是将一个向量从相机坐标系变换到世界坐标系。

位移为相机在世界坐标系的坐标, 旋转为相机位姿的旋转矩阵的转置$R^T$

所以为什么需要多一个转置？旋转矩阵的转置与定义

W2C

通常的计算方法是计算得到C2W的Rt矩阵之后, 直接求逆

    T_{W2C} = np.linalg.inv(Rt)

相机位姿中旋转矩阵的转置与定义

相机的旋转矩阵$R$通常表示：世界坐标系到相机坐标系的旋转

为什么这么定义？

\[Rt = \begin{bmatrix} R^T & t \\ 0 & 1 \end{bmatrix}\]

W2C

Tracking 与 SLAM

Tracking得到的是$W \rightarrow C$的变换, 但是因为物体坐标系与世界坐标系常常被默认为重合, 因此$obj \rightarrow W$被视为$[I

0]$,

\[obj \rightarrow world \rightarrow camera \\ \downarrow \\ obj \rightarrow camera = T_{w2c}T_{o2w}\]

SLAM

\[obj \rightarrow world \leftarrow camera \\ \downarrow \\ obj \rightarrow camera = T^{-1}_{c2w}T_{o2w}\]