pi0
参考:
Maximum Likelihood Training of Score-Based Diffusion Models(NeurIPS 2021)
Flow Matching for Generative Modeling
基础概念
概率路径(probabilty path): 一个随着时间$t\in[0, 1]$变化的概率分布簇${p_t(x)}$
连续正则化流(Continuous Normalizing Flow): CNF是一种生成模型,它的核心思想是通过一个连续时间的可逆变换(flow),把一个简单的分布(如高斯噪声)平滑地“流动”成一个复杂的目标分布(如自然图像)。

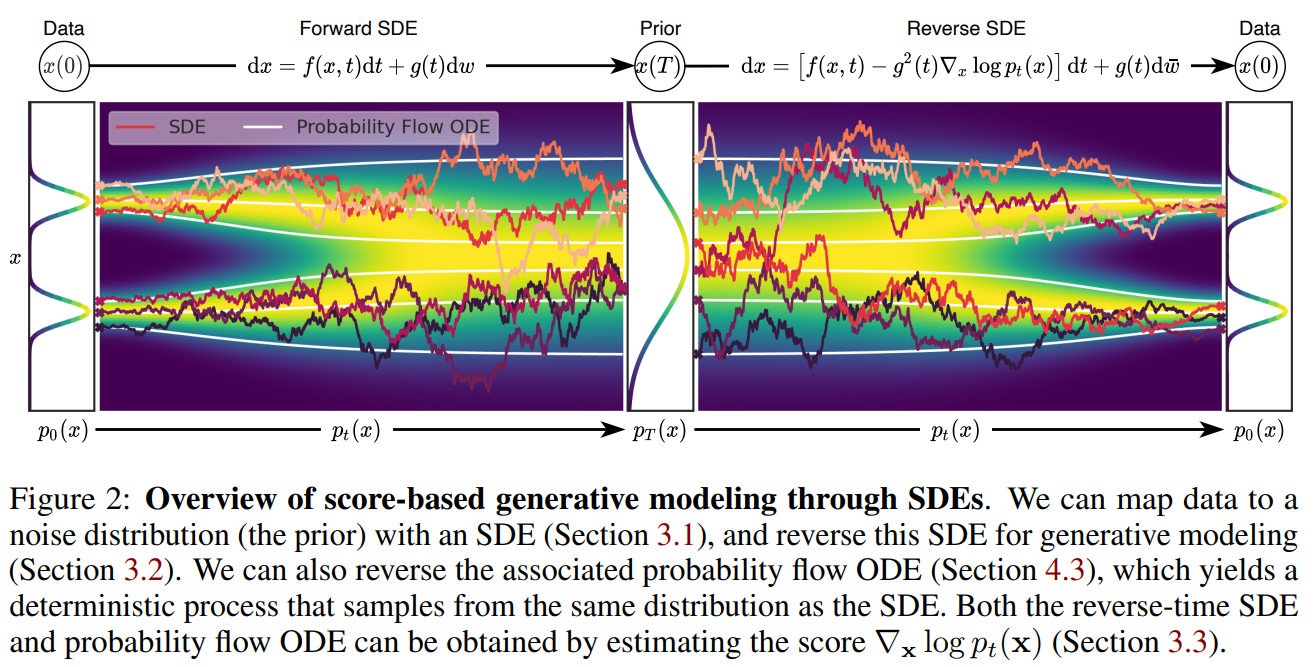
上图为扩散模型的工作原理,上半部分的forward过程(加噪)中,原始数据被添加布朗运动(随机噪声)$\text{d}w$,直至变为高斯噪声。
网络学习的就是下半部分的反向过程:从噪声一步步去噪回原图(反向扩散)。因此,扩散模型本质上是在学习一个“随机微分方程 (SDE)”的逆过程
那么这个扩散过程有什么问题?
慢 训练时:需要在多个时间步上加噪、去噪,通常要训练上百万步。 推理时:生成一张图像要反向积分数百到上千步(如 DDPM 要 1000 步)。 不同随机噪声导致梯度估计方差大,收敛更慢。训练需要平均大量样本才能稳定
因此,CNF的目的就是为了排除掉随机性。数学推导可以证明(见 Song et al., 2021),这里说结论:
1
2
3
对于每一个扩散 SDE,
都存在一个确定性的 ODE(称为 Probability Flow ODE)
它生成的分布族 与 SDE 完全相同。
也就是说:
1
Diffusion (随机) ↔ CNF (确定性)
两者在“概率意义上等价”,只是生成路径不同:
flow matching的公式与对应实现可参考:https://colab.research.google.com/github/gle-bellier/flow-matching/blob/main/Flow_Matching.ipynb
Flow Matching
虽然 CNF 很优雅,但一切并非没有代价,原始CNF的训练需要对ODE进行复杂的数值积分(极慢) 《Flow Matching for Generative Modeling》提出:用 Flow Matching (FM) 的思想来训练 CNF,即直接让神经网络回归一个目标向量场 从而不需要模拟 ODE 也能训练 CNF
这就把 CNF 变成了: 无需仿真(simulation-free) 高效可扩展 可以使用任意类型的概率路径(不再局限于扩散那种)
概念:向量场,流
\[p: [0,1] \times \R^d\rightarrow \R_{>0}\]p是一个映射函数$p(x, t)$
输入:时间$t$(0到1之间)和空间点$x$(d维) 输出:空间点$x$在$t$时刻的概率密度值(正实数)
向量场(vector field)描述了点的运动规律,在$t$时刻点$x$的瞬时速度(一个方向): \(v_t(x) = \R^d\rightarrow\R^d\)
对于任何一个初始点$x$,其轨迹满足微分方程:
\[\frac{d}{dt}x(t) = v_t(x(t))\]初始条件为:
\[x(0) = x_0\]通过积分就能够得到$t$时刻初始点$x_0$的位置$x(t)$
在实践中,我们不仅关注单个点的变化,而是关注所有的样本的分布的变化,空间中的所有点$x$是如何随着时间变化的,前面我们用公式:
\[\frac{d}{dt}x(t) = v_t(x(t))\]可以描述单个点是如何随着时间变化的,那么到了分布中,我们需要引入额外的概念:流
流(flow)是一个映射函数,$\phi_t(x)$表示$t$时刻空间中所有点位置。
\[\phi_t(x): \R^d \rightarrow \R^d\]可以说:flow是由vector field生成的(generated),二者的关系由以下常微分方程定义:
\[\frac{d}{dt}\phi_t(x) = v_t(\phi_t(x))\]初始条件为(0时刻x在原地不动,flow是恒等函数):
\[\phi_0(x) = x\]CNF
因此就有人提出使用神经网络来学习vector field, $v_t(x;\theta)$,其中$\theta$是可学习的参数,即代表深度学习得到的model
$p_t(x)$是一个概率密度函数,与$\phi_t(x)$是一个确定性函数不同,$p_t(x)$的作用就是描述分布,表示样本在空间中的“分布”,不同于$\phi_t(x)$表示的“确定性的位置”。
因为在运动的过程中,vector field可能会压缩/拉伸初始分布,导致即便知道样本在$t$时刻的位置,其分布变化可能很大。
因此,需要一个公式将概率密度分布与已有的flow结合起来,实现:
\[x_0 \sim p_0, x_1 \sim p_1\]现在已经有了公式可以计算点的位置变化:
\[x_1 = \phi_1(x_0)\]需要一个公式$f_t(x)$来实现:
\[p_1 = f_1(p_0)\]flow matching文中的公式3和4就是来实现这个$f_t(x)$的:
\[p_t = [\phi_t]_* p_0\] \[[\phi_t]_* p_0(x) = p_0(\phi_t^{-1}(x)) \det\!\left( \frac{\partial \phi_t^{-1}(x)}{\partial x} \right)\]其中定义了一个push-forward operator,也叫变量代换(change of variables)。其推导来自:概率守恒+ 变量代换公式
对于一个样本$A$,初始时刻和$t$时刻在空间中所有点的概率和应该是不变的。
\[\forall A \subseteq \mathbb{R}^d, \quad \int_A p_t(x)\,dx = \int_{\phi_t^{-1}(A)} p_0(x)\,dx\]当$A=\R^d$时, $\quad \int_A p_t(x)\,dx = \int_{\phi_t^{-1}(A)} p_0(x)\,dx = 1$
应用变量代换,将右边的$\phi_t^{-1}(A)$替换为$A$
$x = \phi_t(x_0)$ 的反函数满足 $x_0 = \phi_t^{-1}(x)$
1维情况下,微元部分的变化为:
\[dx_0 = d\phi_t^{-1}(x) = \left|\frac{d\phi_t^{-1}(x)}{dx}\right|dx\]| $\left | \frac{d\phi_t^{-1}(x)}{dx}\right | $是jacobian修正项,用于修正积分比例。(因为替换后,相当于坐标轴的尺寸发生了变化,乘以一个比例系数才能正确计算) |
到多维情况下, jacobian修正项从一个值变成了行列式:
\[dx_0 = \left| \det\!\left( \frac{\partial \phi_t^{-1}(x)}{\partial x} \right) \right| dx\] \[\int_{\phi_t^{-1}(A)} p_0(x)\,dx = \int_A p_0(\phi_t^{-1}(x)) \left| \det\!\left( \frac{\partial \phi_t^{-1}(x)}{\partial x} \right) \right| dx\]现在融合了概率密度守恒和变量代换,去掉积分部分:
\[p_0(x) = p_0(\phi_t^{-1}(x)) \left| \det\!\left( \frac{\partial \phi_t^{-1}(x)}{\partial x} \right) \right|\]可以发现在最终的结论中,jacobian项的绝对值号没了,因为$\phi_t(x)$始终满足smooth, invertible,因此其jacobian行列式在整个空间上不会改变方向,绝对值号可以去掉
\[[\phi_t]_* p_0(x) = p_0(\phi_t^{-1}(x)) \det\!\left( \frac{\partial \phi_t^{-1}(x)}{\partial x} \right)\]本身这个绝对值号就是为了避免出现负号而引入的,因为体积等概念不应该出现负
前面提到了flow是由vector field generated,p_t(x)则是由flow进一步生成的。$p_t$被称为概率密度路径(probability density path)
A vector field $v_t$ is said to generate a probability density path $p_t$ if its flow $\phi_t$ satisfies equation: $p_t = [\phi_t]_* p_0$
v_t(x)定义了位置的移动(ODE),p_t满足连续性方程(PDE)
density path $p$
在初始时, prior density path $p_0$是一个纯噪声,基于该prior,CNF的
% — Change of variables formula — \begin{equation}
\label{eq:change_of_variables_integral} \end{equation}
% — Equating integrands (probability conservation holds for all regions A) — \begin{equation} p_t(x) = p_0(\phi_t^{-1}(x)) \left| \det!\left( \frac{\partial \phi_t^{-1}(x)}{\partial x} \right) \right| \label{eq:pushforward_density} \end{equation}
% — Simplified form: definition of push-forward operator (Equation 4) — \begin{equation} [\phi_t]_* p_0(x) = p_0(\phi_t^{-1}(x)) \det!\left( \frac{\partial \phi_t^{-1}(x)}{\partial x} \right) \label{eq:pushforward_def} \end{equation}