球谐函数与颜色(Spherical Harmonics & Color)
RGB转换为球谐波SH, 转换函数似乎很简单, 而且转换前后都是(n, 3), 这很难不让人好奇:
- 球谐函数到底与RGB有什么不同?
- 参数C0是如何确定的?
1
2
3
4
5
6
7
C0 = 0.28209479177387814
def RGB2SH(rgb):
return (rgb - 0.5) / C0
def SH2RGB(sh):
return sh * C0 + 0.5
先给出回答:
- 在球谐波表示中, (C_0) 是一个常数,用于归一化最低阶(零阶)的球谐波函数 (Y_{00})。零阶球谐波函数 (Y_{00}) 是一个常数,与方向无关,其值通常设为 (\sqrt{1/4\pi}),数值近似为 0.28209479177387814。这个常数是从球谐波函数的正交性和归一化条件中得出的。 SH的三个维度代表RGB三个通道的球谐波系数
论文中提到,优化3D高斯的参数来获得隐式表达,这些参数包括:位置、协方差、透明度$\alpha$、球面谐波系数(SH coefficients)以及高斯密度的自适应控制
球谐函数来表达颜色,可以表达依赖于视角的颜色(view dependent color)。 reference
球谐函数
球谐(Spherical Harmonics)函数是一组基函数,通常用于表示球面上的函数。在计算机图形学中,球谐函数被广泛应用于光照和反射模型中,用来表示光照或反射的强度分布。
基函数
基函数其实是一个相对的概念,类似于空间中的基向量,基向量可以通过组合表示张成的空间中的所有向量。同理,基函数也可以通过线性or非线性组合来表示其张成的函数空间的函数, 傅里叶变换、球面谐波都是常见的基函数线性组合为原函数。
投射、正交、叉乘、点乘
Q:什么是”投射”?什么是函数叉乘?为什么叉乘能够得到基函数对应的系数$c_i$
以该文为例,很多中文的内容上会使用”投射”这种描述,其实对应着英文中的project, 投影, 投射其实都是翻译的不同。
基函数(Basis function)是可以通过调整比例(权重)然后互相组合来形成原函数近似的简单函数。通过将原函数project到不同的基函数上得到每个基函数对应的系数。
基函数正交性
函数的正交性: (连续情况下)如果满足 $\int^{b}_{a}f(t)g(t)dt=0$ ,我们称函数$f(t)$和$g(t)$在给定的区间(定义域)$[a,b]$上是正交的。
利用基函数的正交性可以来计算基函数的系数
bg:线性基函数与非线性基函数
线性基函数
基函数的形式本涉及到基函数之间的乘积或其他非线性操作。常见的线性基函数就是多项式基函数。
一次多项式基函数:$f(x) = ax + b$
二次多项式基函数:$f(x) = ax^2 + bx + c$
线性基函数并非是只有一个基函数,其可以包含多个基函数,但是每个基函数都是关于输入变量($x$)的线性函数。例如线性基函数$f(x) = ax + b$就是由基函数$y=x$和$y=1$通过常数系数$a$和$b$组合成的。$y=x$是关于$x$的线性函数,$y=1$是常数函数,都是线性的。因此其线性组合成的
非线性基函数
非线性基函数,基函数自身是非线性的或者基函数之间进行了非线性操作。
高斯基函数:$f(x) = e^{-\frac{(x - \mu)^2}{2\sigma^2}}$
sigmoid 基函数:$f(x) = \frac{1}{1 + e^{-x}}$
多项式基函数:$f(x) = x^2, x^3, x^4, …$
#
总之,球谐函数的结构由其次数 l 和阶 m 决定,其中 l 表征对极角的函数依赖性,m 表征对方位角的依赖性。前三个系数也称为高斯系数,在特定l度内对结构的变化起作用。操纵 l 和 m 可以影响谐波的结构,使用 Hummingbird Exceed/Open Exceed 等程序可以显示这些变化。除了更常用的指数基之外,高斯系数还经常用作球谐函数的基。
Reference: https://www.physicsforums.com/threads/spherical-harmonics-degree-l-order-m-structure-variation.805217/
论文中关于颜色的消融实验
根据github的issue
the 0th band is a constant color for all directions. Effectively we set the band to 0 for the ablation, so we just optimized an RGB color value.
以及另一个issue
Parameters f_dc_0, f_dc_1, f_dc_2 contain your R, G and B colors, You need to convert them into regular format with something like R = 0.5 + C0 * f_dc_0 where C0 is the zeroth-order spherical harmonic coefficient. After that, you will obtain colors in the [0, 1] range and it is straightforward to map them to [0, 255] integers.
reference repo
3d gaussian splatting论文中提到其关于谐波函数的实现遵循前两篇论文
Plenoxels: Radiance Fields without Neural Networks
Instant Neural Graphics Primitives with a Multiresolution Hash Encoding
The directional appearance component (color) of the radiance field is represented via spherical harmonics (SH), following standard practice [Fridovich-Keil and Yu et al. 2022; Müller et al. 2022].
参考
paper
ISSUE-728 Meaning of features_dc and features_rest中推测: feature_dc代表diffuse color, 球谐函数的最低阶, 完全不考虑其他光照的作用的话, 就是物体本身的颜色. rest代表剩余的(rest)其他SH系数.
还提到了一篇文献Spherical Harmonic Lighting: The Gritty Details
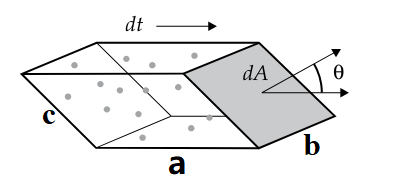
随着$\theta$的增大, 体积V逐渐减小。光的通量密度(Flux Density), 是单位面积有多少光子与静止表面相接触。可以看到, 与图中的$\theta$成cos关系。
\[V=abc\cos{\theta}\]参考该paper: 其中page.3的渲染公式
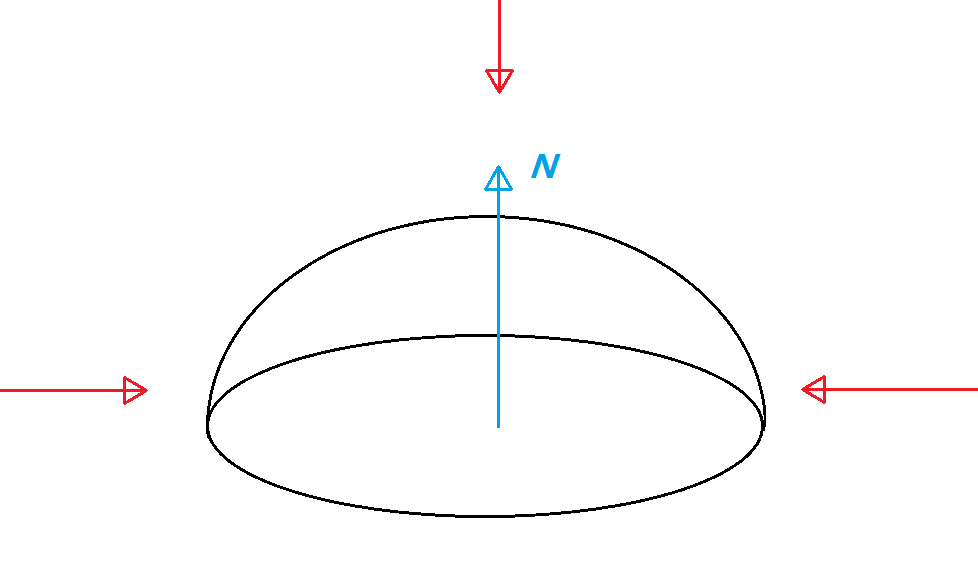
\[L(x, \omega_o) = L_e(x, \omega_o) + \int_{S} f_r(x, \omega_i \rightarrow \omega_o) L(x', \omega_i) G(x, x') V(x, x') d\omega_i\]For each light source the intensity (often expressed as an RGB colour) is multiplied by the scalar dot product between the unit surface normal $N$ and the unit vector towards the light source $L$.
光源的强度(intensity), 通常翻译为强度/光强, 通常也被表示为RGB颜色.
这说明了一个很简单的问题, 空间中一个点$x$在方向$\omega_o$观察到的最终颜色(强度)$L(x, \omega_o)$, 受到两部分的影响: 自身原本的光亮度$L_e(x, \omega_o)$ 和 反射到该观察方向的光亮度$\int_{S} f_r(x, \omega_i \rightarrow \omega_o) L(x’, \omega_i) G(x, x’) V(x, x’) d\omega_i$。
其中第二项继续拆分, 我们先跳过积分阶段:
$f_r(x, \omega_i \rightarrow \omega_o)$是$x$处的BRDF(双向反射分布函数, Bidirectional Reflectance Distribution Function), 之前page.1中的漫反射函数其实就是一个简单的BRDF。描述了位置$x$处, 从方向$\omega_i$入射的光线反射到$\omega_o$的的程度。
$L(x’, \omega_i)$表示从另一个位置$x’$(可能是光源也可能是其他的可反射的表面)沿着$\omega_i$来到的光强,
$G(x, x’)$和$V(x, x’)$分别代表阻挡/衰减程度以及可见性(是否可见)
所以论文中提到的渲染方程存在的问题就很好理解了:
The problem with the rendering equation is that it is difficult to compute, and definitely not a real-time friendly operation. It is an integral over a hemisphere of directions where $L$.
因为要计算来自其他光源/表面的光线, 必须计算来自所有可能的方向的光线, 这也是渲染函数中的第二部分积分的来源, 因为$x$是一个表面的位置, 因此只能接收到来自法向一定夹角的光, 所以积分的区间是一个半球。
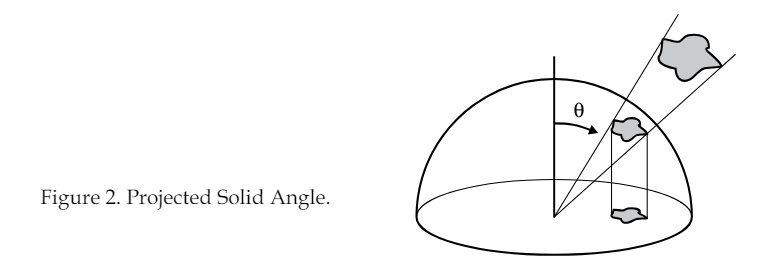
其中提到了”Project Solid Angle”(固体投影角), 在三维空间中衡量一个表面的点能够接收到来自某个方向的光线量的度量。在计算光照的时候,能够帮助确定光照打在平面上的有效面积。其实就说明了一个很简单的道理:投影固体角在计算光照时帮助确定光线打在物体上的有效面积,特别是当光线与物体表面成一定角度时。这个角度越大(即光线与表面法线越接近平行),表面接收到的光量就越少。 具体来说,当光线正对表面时(即法线与光线方向一致),余弦值为1,表面接收到最大光量;当光线与表面平行时(余弦值为0),表面接收不到任何光。
这也是为什么文中有这么一句话: “This is the reason behind the cosine (or dot product) in the diffuse shading equation. “ 使用”单位方向向量点积”->”计算余弦值”,允许漫反射模型简单且有效地模拟光线如何根据不同角度影响物体表面的亮度。
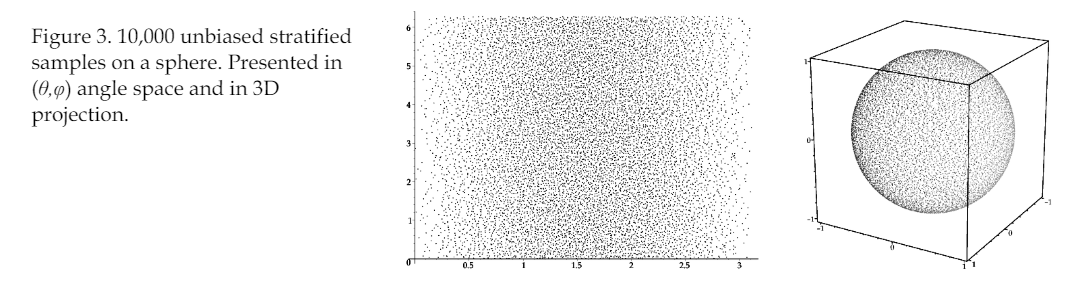
为了能够在半球上进行积分, 在球面上进行随机采样, 创建两个Independent canonical random numbers, 即在[0, 1)区间内均匀分布的随机数。
计算极角$\theta$和方位角$\phi$
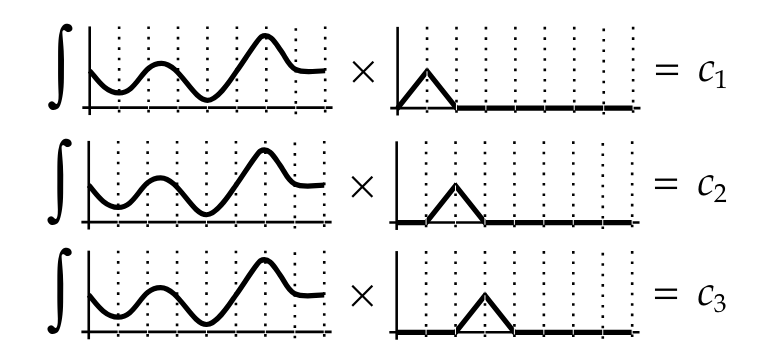
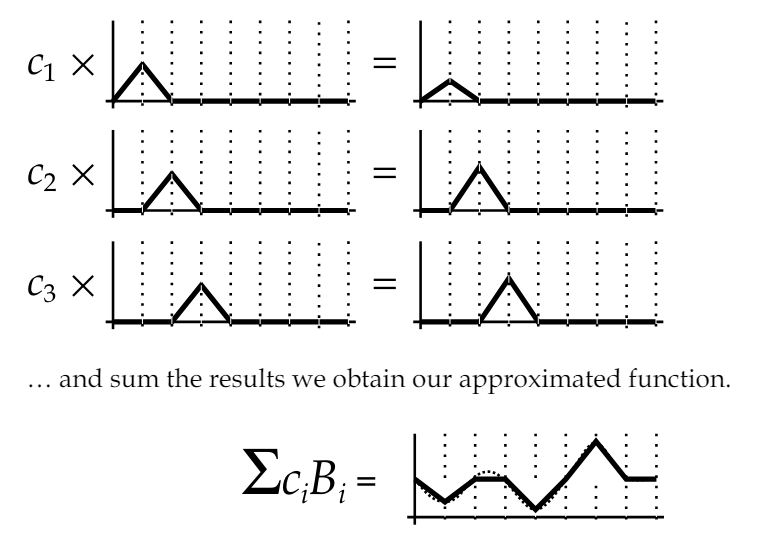
\[\theta = 2 \arccos(\sqrt{1 - \xi_x})\] \[\phi = 2 \pi \xi_y\] \[(2 \arccos(\sqrt{1 - \xi_x}), 2 \pi \xi_y) \rightarrow (\theta, \phi)\]然后是基函数部分, “Basis functions are small pieces of signal that can be scaled and combined to produce an approximation to an original function”, 这里所谓的scaled和combined其实就是指基函数的加权和相加。
“and the process of working out how much of each basis function to sum is called projection.” 计算每个基函数的权重的过程, 称为project. 结合之前的”投射”计算SH系数来理解。
通过对原函数$f(x)$与基函数$b_i(x)$的乘积进行积分来计算基函数的系数$c_i$
\[c_i = \frac{\int_a^b f(x) b_i(x) \, dx}{\|b_i\|^2}\]利用基函数的正交性, $f(x)$与基函数$b_i(x)$的乘积只会保留与$b_i(x)$的相关项, 对于$f(x)$中的其他项$b_j(x), i \neq j$因为基函数的正交性会变为0. 除以$b_i(x)$的平方积分后, 就能够获得$f(x)$中$b_i(x)$的系数$c_i$。
基函数$b_i(x)$的范数$|b_i|$定义为:
\[\|b_i\|^2 = \int_a^b b_i(x)^2 \, dx\] \[c_i = \frac{\int_a^b f(x) b_i(x) \, dx}{\int_a^b b_i(x)^2 \, dx}\]如果基函数的归一化的(基函数的范数都是1), 那么公式还可以继续简化。这也是为什么在算法实现时经常使用归一化的正交基函数。
\[c_i = \int_a^b f(x) b_i(x) \, dx\]而且这一切都能在向量空间中找到对应的影子: 数学, 很神奇吧!
正交基函数之间的内积为0, 他们彼此独立, 互相不影响。我们常说的傅里叶变换, sin和cos就是一种基函数。
基函数->正交多项式(任意两个乘积积分: 不同->返回0, 相同->常数值)->要求返回的结果是0或1->正交基函数
这些多项式族通常以研究他们的数学家的名字命名, Chebyshev, Jacobi and Hermite, 本文中, 更关心的是伴随勒让德多项式(Associated Legendre Polynomials)
球面坐标
球面坐标也是三维空间中的坐标系统, 其包含$(r, \theta, \phi)$, 分别代表径向坐标, 极角和方位角, $\theta$通常在$[0, \pi]$范围内, $\phi$通常在$[0, 2\pi)$或者$[-\pi, \pi)$范围内。 而在我们的情况中, 目前的半球
 来源:wiki-Spherical coordinate system
来源:wiki-Spherical coordinate system
勒让德多项式与球面谐波
勒让德多项式是球面谐波的核心, 球面谐波是一个球面上定义的数学系统, 类似于傅里叶变换。 SH函数定义在虚数上, 但是我们只对近似球面上的实函数(光强场, light intensity fields)感兴趣。因此当我们提到SH时, 我们只考虑实球面谐波函数(Real Spherical Harmonic function)。
勒让德多项式在$[-1, 1]$区间上具有正交性。
勒让德多项式(Legendre Polynomials) \(P_l(x) = \frac{1}{2^l l!} \frac{d^l}{dx^l} \left( x^2 - 1 \right)^l\)
相关勒让德多项式(Associated Legendre Polynomials)在原来的基础上添加了额外的参数$m$, 主要是为了在球坐标系中进行扩展。其中的$(1-x^2)^{m/2}$是其权重因子, 可以使相关勒让德多项式满足正交性。 \(P_l^m(x) = (1-x^2)^{m/2} \frac{d^m}{dx^m} P_l(x)\)
其中$l$是非负整数, 而后添加的自变量$m$取$[0, l]$范围内的数值,
添加额外的参数是为了能够同时控制球面坐标的$\phi$和$\theta$, 权重项其实是$\sin^m(\theta)$的表达式, 在区间$[-1, 1]$上校正函数的分布(对应着极角从0到π)
前面我们先均匀采样了球面坐标$(\theta, \phi)$, 现在可以将其转换到笛卡尔坐标$(x,y,z)$
\[\]