文章

attention is all you need to learn

发表于
作者
20 分钟阅读

[toc]

学习和使用Transformer很久了, 很多地方的理解都比较混乱，因为学习的资料和使用的模块在很多部分已经不同步了。一直想按照时间顺序串一下Transformer的演化过程，就趁着这个春节的时间，一直推到ViT为止吧。

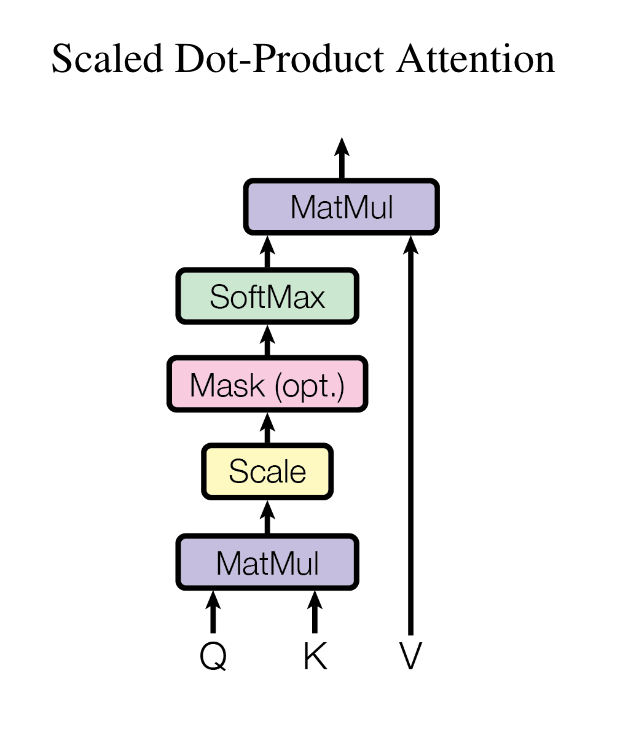
Scaled Dot-Product Attention

以下公式来自Attention Is All You Need (2017)

1.输入一个序列，包含n个元素，将这n个word通过线性变换, $W_Q, W_K, W_V$得到我们的主角$Q,K,V$.也大概理解了为什么很多的教程以NLP任务举例, 因为最早的注意力提出来就是为了解决NLP任务的, 像是ViT等是后来才出现的。

对于Q中每一个向量$q_i$，计算与K中所有$k_j$的相似性，对应到注意力的基础公式, query与key计算特征相似度, 这一点在feature match中都是非常常见的操作了。

\[\textit{Attention Score}(Q, K) = Q K^T\]

但我们能发现，论文中的注意力公式多一个缩放因子$\sqrt{d}$作为分母

\[\textit{Scaled Attention Score}(Q, K) = \frac{Q K^T}{\sqrt{d}}\]

alt text

From: Attention Is All You Need, Figure 2: (left) Scaled Dot-Product Attention.

MatMul: $QK^T$

Scale: $\frac{1}{\sqrt{d}}$

可以发现, 公式中并没有Mask这一部分，(opt.)也表明它是可选的。这部分在Decoder中的self-attn中会被使用到。

缩放因子的作用

一般来说, 一个网络中的特征维度d是一个固定值, 因此相当于对Q和K的相似度除以了一个固定值, 这个值是随着网络的特征维度而改变的, 即$\sqrt{d}$是维度相关的缩放因子。它的作用是缩小点积的极端值，使得注意力得分在经过softmax之后输出的结果更加平缓。

举个最简单的例子:

假设输入经过线性变换后得到: \(q_1 = [1, 0, 1, 0] \\ q_2 = [0, 1, 0, 1] \\ k_1 = [1, 0, 1, 0] \\ k_2 = [0, 1, 0, 1]\)

计算$Q \cdot K^T$

\[Q \cdot K^T = \begin{pmatrix} q_1 \cdot k_1 & q_1 \cdot k_2 \\ q_2 \cdot k_1 & q_2 \cdot k_2 \end{pmatrix} = \begin{pmatrix} 2 & 0 \\ 0 & 2 \end{pmatrix}\] \[softmax(Q \cdot K^T)=\begin{pmatrix} 0.88 & 0.12 \\ 0.12 & 0.88 \end{pmatrix}\]

如果添加了缩放因子$\sqrt{d}$

\[softmax(\frac{Q \cdot K^T}{\sqrt{d}}) = softmax\begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} =\begin{pmatrix} 0.73 & 0.27 \\ 0.27 & 0.73 \end{pmatrix}\]

可以发现, scaled attention score相比于不带缩放因子的版本, 相似度分数的差异更小了。那么$\sqrt{d}$是否可以替换为常量？当然可以, 但最好还是跟随维度来进行变化, 因为不同的任务中向量的维度可能差异非常大, 如果缩放因子过大或过小, 都不能够达到缩小极端值的效果。

使用$Q,K$计算相似度并输入softmax，借助其非线性特征进行归一化和平滑后, 作为注意力权重, 计算与$V$的加权，至此就是我们所熟悉的注意力公式:

\[\textit{Attention}(Q, K, V)=softmax(\frac{Q \cdot K^T}{\sqrt{d}})V\]

其实缩放因子这个东西本身是为点乘注意力(dot-product attention)而服务的, 是为了克服特征维度$d$的影响，有的公式中也会强调$d$是K的维度$d_k$, 但是就目前看到的大部分实现来说, $Q$和$K$的维度$d_q$和$d_k$通常是相同的，因为便于计算。因此缩放这部分是有点偏经验向的东西。可以参考原文中的描述：

注意力与梯度消失

1

注意力通常可以解决梯度消失问题, 因为其在encoder status与decoder之间建立了直接连接。与CNN中的跳连接非常相似。

梯度消失是因为网络过深时，反向传播计算的梯度很小，导致前面的层难以更新权重。在传统的RNN, LSTM等序列模型中非常常见。

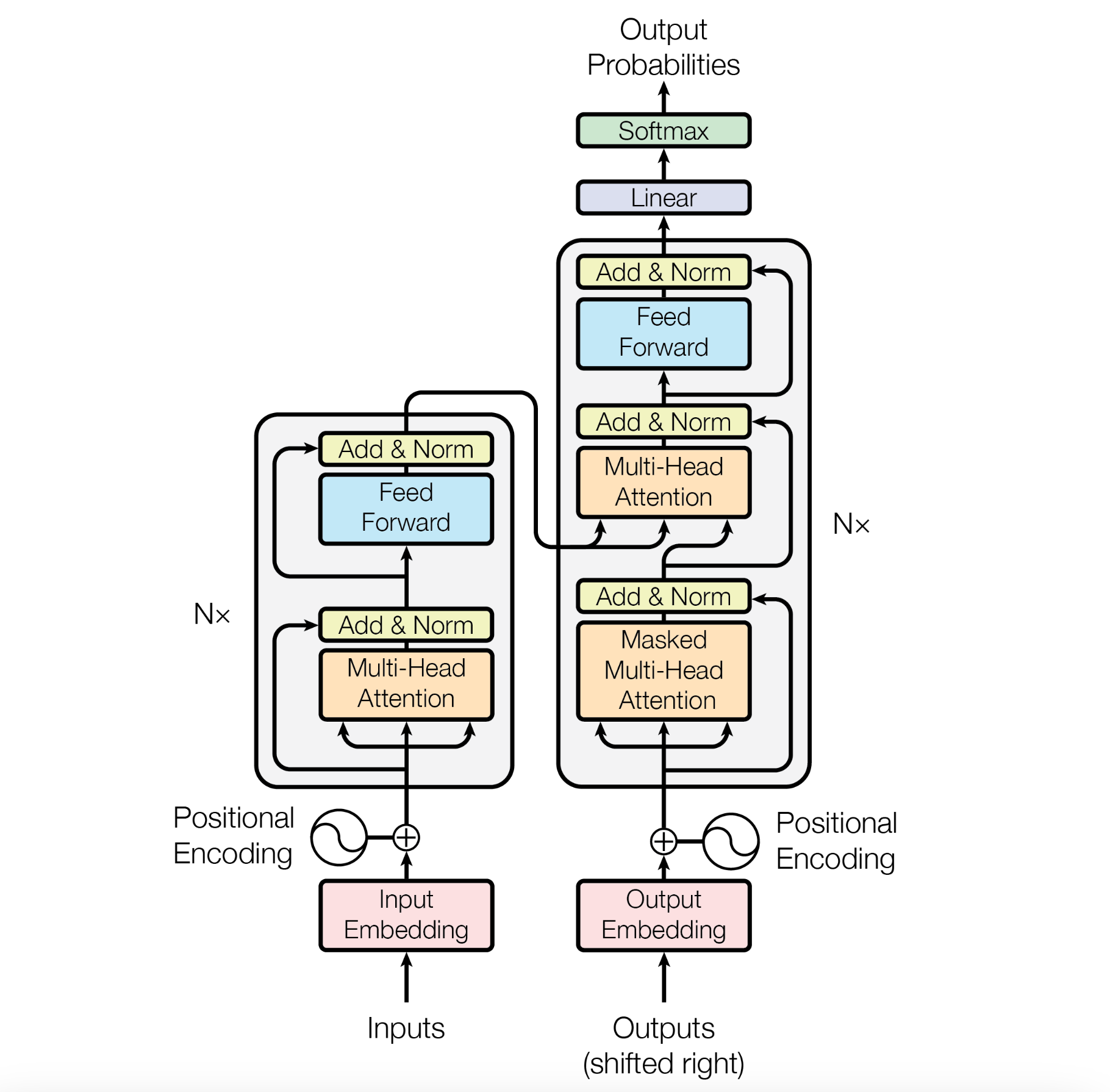
alt text

From: Attention Is All You Need, Figure 1: The Transformer - model architecture.

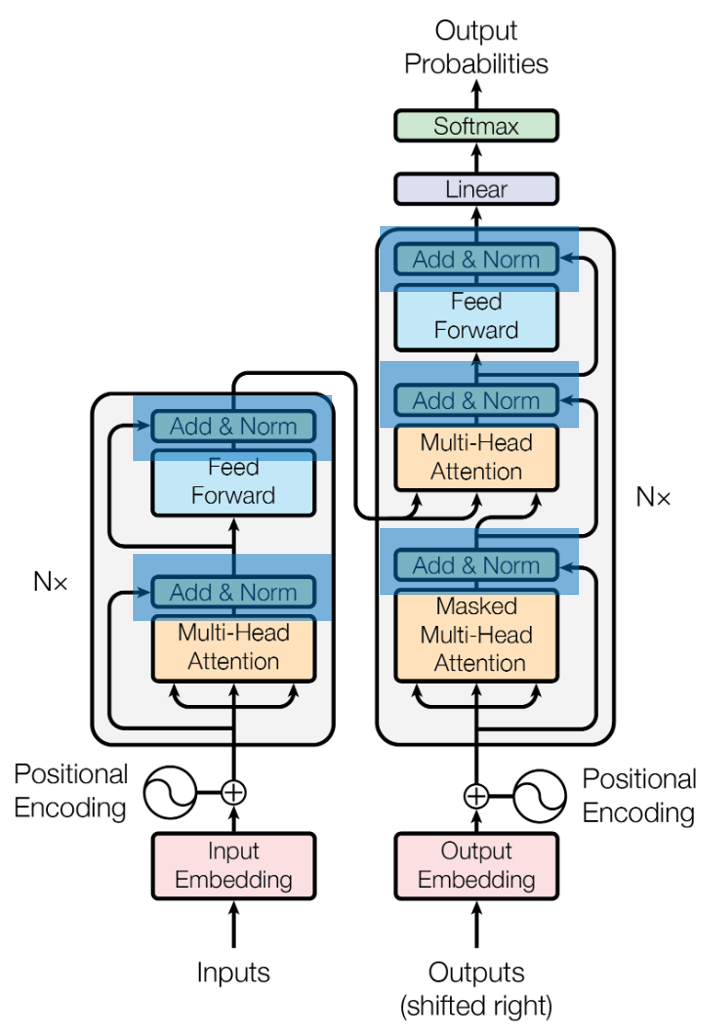
观察transformer的结构图我们可以发现：encoder的输出直接连接到decoder的MHA的输入。

self-attn与cross-attn

结构图中, 左侧Encoder和右侧Decoder的第一个MHA都是自注意力机制，其用于计算输入序列内部注意力和关系，而Decoder中的第二个注意力，输入分别来自输入序列和输出序列的结果，为cross-attn, 跨模态交换信息。

Masked MHA

可以注意到, Decoder的第一个MHA是Masked MHA, 其中的mask是为了保持自回归(auto-regressive)特性。

解码器的自注意力必须避免未来信息的泄露，确保模型在生成第 𝑡 个 token 时，只能依赖 𝑡 之前的信息，而不能提前看到未来的 token。

如何理解？

其实应该这么理解: 以 语言翻译 为例,

输入（English）: I love apple 目标（Chinese）: 我 喜欢 苹果

Decoder中的第一个Mask MHA其实是在学习目标语言之间的语法等关系，而第二MHA（cross-attn）才是学习两种语言之间的映射，因此，在Decoder的第一个Mask MHA中, “我”不应该能看到”喜欢”和”苹果”, “喜欢”不能看到”苹果”, 否则就相当于提前看到了答案, 变成了对数据集的拟合。

那么还剩下一个问题, 在Mask MHA中, mask是如何添加的？（具体操作而言）

实现起来就更简单了，直接在计算用于加权的相似度得分时， 如果对应的元素是来自未来的, 直接将其置为0, 不允许其参与计算即可。

例如:

Encoder中:

\[\text{Output}_{I}=\alpha_{I, I}V_{I} + \alpha_{I, love}V_{love} + \alpha_{I, apple}V_{apple}\]

Decoder的mask self-attn中:

\[\text{Output}_{我}=\alpha_{我, 我}V_{我} + \alpha_{我, 喜欢}V_{喜欢} + \alpha_{我, 苹果}V_{苹果}\] \[\alpha_{我, 喜欢}V_{喜欢} = 0, \alpha_{我, 苹果} = 0\]

不允许未来的元素参与计算。

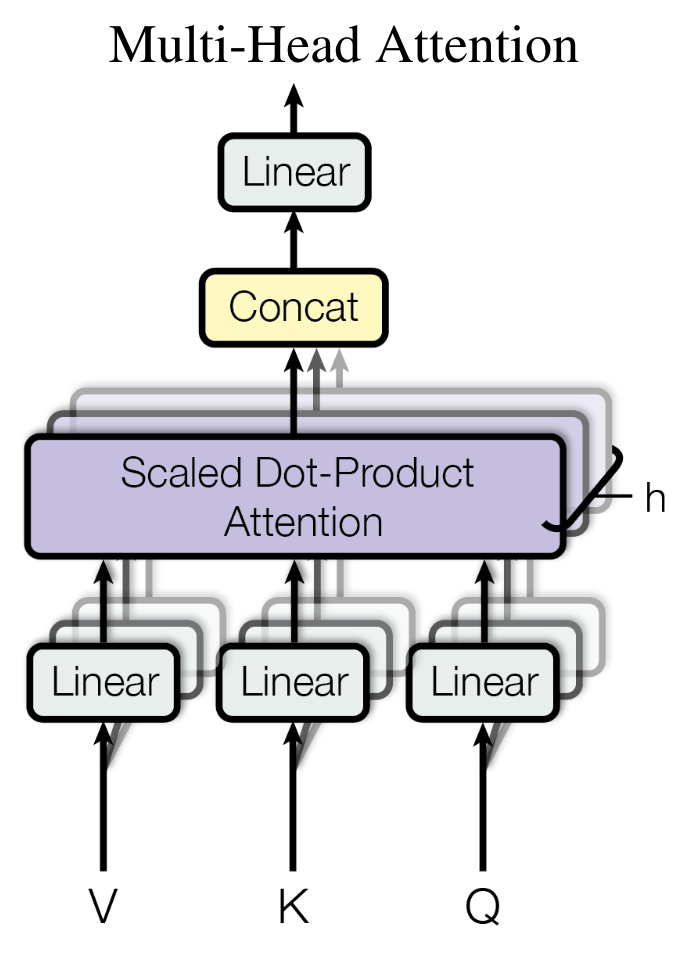
MHA(Multi-Head Attention)

Multi-head是如何出现的?

根据上述的注意力公式, 输入

假设输入序列的长度为$n$, 矩阵$Q, K, V$的shape分别为$\mathbb{R}^{n \times d_q}$, $\mathbb{R}^{n \times d_k}$, $\mathbb{R}^{n \times d_v}$

最终得到的加权和维度也是$\mathbb{R}^{n \times d_v}$

举具体例子,

输入:

长度为$n$的序列, 得到shape分别为$\R^{n \times d_q}$, $\R^{n \times d_k}$, $\R^{n \times d_v}$的矩阵$Q, K, V$(因为Q和K要进行点积操作, 所以要满足$d_q=d_k$, 但很多情况下, $d_v$与$d_q, d_k$也是相同的) 最终得到的加权和计算得到的加权和维度也是$\R^{n \times d_v}$

Q:多头注意力是如何实现的？

A:分别使用$h$个独立的线性变换$W_i(i=1, 2, …, h)$ 将$Q, K, V$进行线性变换。

若有$h$个头, 每个头的维度是$d_h$ \(d_h = \frac{d}{h}\)

对进行线性变换 \(Q' = QW_h\)

\[(n, hd_h) \larr (n, d_q) × (d_q, hd_h) \larr (n, d_q)×(d_q, d)\]

对$K, V$进行同样的处理

之后有一个阶段, 划分头

$d$称为多头注意力的嵌入维度(representation dimensionality)(多头注意力总维度), $h$是头的数量,

\[Q_h = \text{reshape}(Q', (h, n, d_h))\]

划分后每个头有一个独立的key, query, value集合, 在单独的子空间中计算。

\[\text{Attention}_i = softmax(\frac{Q^i_h \cdot {K^i_h}^T}{\sqrt{d_h}})V^i_h, i=1,...,h\]

$h$个头, 每个头输出的维度是$(n, d_h)$

将$h$个头的输出concat, 得到$(n, hd_h)$维度的输出。拼接后结果经过一个线性变换得到最终输出。

\[O = \text{concat}(O_1, O_2, ..., O_h)\]

整个过程可以被简化：

$Q’=QW_h$和$Q=XW_q$两步操作可以合并为一步$Q’=XW^Q_h$，一般会写成$Q_h=XW^Q_h$，但是从$Q’$到$Q_h$其实还差了一步reshape操作 $Q_h=\text{reshape}(Q’)$

\[Q'=XW_qW_h\] \[(n, hd) \larr (n, c) × (c, d_q) × (d_q, hd_h)\] \[Q_h = \text{reshape}(Q', (h, n, d_h))\]

一般情况下, 最终reshape的$(B, H, N, d_k)$实现是更常见的。

得到多头输出后

首先计算注意力分数

\[A_h=softmax(\frac{Q_h \cdot K_h^T}{\sqrt{d}})\]

$Q_h: (B, H, N, d_h)$

$K_h^T: (B, H, d_h, N)$ 交换最后两个维度

最终得到注意力分数$A_h$的shape为$(B, H, N, N)$

加权计算后得到$O_h:(B, H, N, d_h)$

\[O_h = A_hV_h\]

拼接多头输出

\[O = \text{concat}(O_1, O_2, ..., O_H)\]

拼接这一步通常是一个维度交换+reshape实现的

$\text{permute}(0, 2, 1, 3):(B, H, N, d_h) \rarr (B, N, H, d_h)$

$\text{reshape}(B, N, hd_h):(B, N, H, d_h) \rarr (B, N, hd_h) \rarr (B, N, d)$

综上可以发现, 将多头的输出经过permute操作变为$(B, H, N, d_h)$是为了方便先进行注意力分数计算, 等拼接时再去reshape。

alt text

From: Attention Is All You Need, Figure 2: (right) Multi-Head Attention consists of several attention layers running in parallel.

为什么要使用多头机制？

  1. 并行计算 通过MHA的结构图很容易发现, 不同的head注意力计算是可以并行的。

  2. 能够映射特征到更多的子空间 使模型从不同的视角学习特征来增强表达能力，这个所谓的不同视角，是”h个头使用独立的线性变换”实现的, 即 h个头在映射QKV时使用的$W_q, W_k, W_v$是不同的, 以保证其计算的梯度不同$\rarr$优化的方向不同$\rarr$各个头映射到的子空间不同

根据论文中的描述:

首先: 将qkv的值通过$h$次不同的学习到的线性变换得到$d_k, d_k, d_v$维的输入, 比直接使用相同的$d_{model}$维的输入效果要好。在每一次线性投影后的结果上计算注意力

Transformer

分析完了attention, 我们回到最开始transformer的结构图

alt text

From: Attention Is All You Need, Figure 1: The Transformer - model architecture.

以NLP举例, 输入”I am human”

Input Embedding 将三个原始输入通过嵌入层(Embedding Layer)转换为指定维度(d=512)的向量(3, 512)

Positional Encoding 位置编码为每个嵌入向量添加位置编码。例如$X_i=E_i+{PE}i, $ $E_i \in \mathbb{R}^{d{model}}$为Embedding后提取的向量, ${PE}i \in \mathbb{R}^{d{model}}$为位置编码。(需要位置编码是因为Transformer不像RNN和LSTM等模型一样有隐向量和递归结构。递归本身就隐含了位置/顺序关系)

MHA self-attention计算, “I”, “am”, “human”在每个head, 会通过各自独立的$W^Q, W^K, W^V$计算得到各自的三个表示$Q, K, V$, 不同向量之间互相计算关系权重以理解不同向量之间的依赖关系。

每个向量对应的输入是其与其他向量（包括自身）的注意力权重加权后的结果。

\[\text{Output}_{I}=\alpha_{I, I}V_{I} + \alpha_{I, am}V_{am} + \alpha_{I, human}V_{human}\]

Feed Forward Fully-connected feed-forward network, 对每一个位置(词)进行独立的线性变换。根据论文中的描述是线性变换($512 \rarr 2048$)+ReLU(激活层)+线性变换($204 8\rarr 512$)

\[FFN(x)=max(0, xW_1+b_1)W_2 + b_2\]

先映射到更高维度, 通过激活层激活，然后映射回原本维度。一是为了映射到更高维度增强表示能力，二是通过激活层引入模型的非线性变换以捕获更复杂的输入模式。

Add&Norm 残差连接和归一化主要是为了防止梯度消失/梯度爆炸和维持数值稳定性。

Decoder部分

在初步学习的时候, 很容易将transformer的结构与传统的seq2seq划上等号。实际上，transformer的Encoder和Decoder不是类似于”$A \rightarrow \text{Encoder} \rightarrow B, B \rightarrow \text{Decoder} \rightarrow A$”的结构。

还是以”我是人类”和”I am human”的翻译为例子

I, am, human 拆分为word元素, 在翻译任务中, 会实现创建好词表Vocabulary, 词表负责映射 单词 和 下标, 下标 用于去Embedding矩阵中读取对应的d维向量（当然现代的NLP模型为了防止Embedding矩阵变得巨大, 往往会使用子词、字节对编码BPE等方式来压缩，在这里就不深入了）

经过Embedding层之后, 各个词对应的向量在附加位置编码，然后输入到MHA中, 根据多头注意力得分加权注意力求和, 得到各个词加权后对应的向量。

Transformer为什么没有如RNN中的bias？

问出这个问题，其实是没有理解Transformer的QKV是为了做什么。

在RNN中, 我们使用如下的公式:

\[h_t = \text{Activation}(W_x x + W_h h_{t-1}+b)\]

Activation是一个非线性激活函数, 比如tanh或者ReLU. 之所以管$h_t$叫隐藏状态(Hidden State)，是因为它是一个中间结果，既不是网络的输入也不是网络的输出，是网络整个黑盒中的一部分。

之所以RNN会有偏置项$b$, 是为了防止零输入导致的输出相同。

手撕Transformer

Croco中的attention

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

class Attention(nn.Module):
    def __init__(self, dim, rope=None, num_heads=8, qkv_bias=False, attn_drop=0., proj_drop=0.):
        super().__init__()
        self.num_heads = num_heads
        head_dim = dim // num_heads
        self.scale = head_dim ** -0.5
        self.qkv = nn.Linear(dim, dim * 3, bias=qkv_bias)
        self.attn_drop = nn.Dropout(attn_drop)
        self.proj = nn.Linear(dim, dim)
        self.proj_drop = nn.Dropout(proj_drop)
        self.rope = rope 

    def forward(self, x, xpos):
        B, N, C = x.shape

        qkv = self.qkv(x).reshape(B, N, 3, self.num_heads, C // self.num_heads).transpose(1,3)
        q, k, v = [qkv[:,:,i] for i in range(3)]
        # q,k,v = qkv.unbind(2)  # make torchscript happy (cannot use tensor as tuple)
               
        if self.rope is not None:
            q = self.rope(q, xpos)
            k = self.rope(k, xpos)
               
        attn = (q @ k.transpose(-2, -1)) * self.scale
        attn = attn.softmax(dim=-1)
        attn = self.attn_drop(attn)

        x = (attn @ v).transpose(1, 2).reshape(B, N, C)
        x = self.proj(x)
        x = self.proj_drop(x)
        return x

Residual Connection

残差连接是Transformer架构中非常常见的技术。将输入结果通过一个跳跃连接(skip connection, 最早由ResNet提出)连接到子层的输出上。

\[Output = Layer(x) + x\]

我们之前看过的不论是self-attn还是cross-attn的Transformer都能看到它的身影。

1
2
3
4
5
6
7
8
9
10
11
12
13

    # self-attn + MLP
    def forward(self, x, xpos):
        x = x + self.drop_path(self.attn(self.norm1(x), xpos))
        x = x + self.drop_path(self.mlp(self.norm2(x)))
        return x

    # self-attn + cross-attn + MLP
    def forward(self, x, y, xpos, ypos):
        x = x + self.drop_path(self.attn(self.norm1(x), xpos))
        y_ = self.norm_y(y)
        x = x + self.drop_path(self.cross_attn(self.norm2(x), y_, y_, xpos, ypos))
        x = x + self.drop_path(self.mlp(self.norm3(x)))
        return x, y

在最早的Transformer架构中我们可以发现, Add(也就是Residual Connection)和Norm是一起使用的。主要出现两部分输出之后：多头注意力(Multi-Head Attention, MHA)和前馈神经网络(Feed-Forward Neural Network), 这两个残差连接会和归一化一起使用(Layer Normalization), 使得Transformer能够更深地堆叠多个encoder和decoder, 而不会出现梯度消失或信息丢失。

Net
Net
本文由作者按照 CC BY 4.0 进行授权