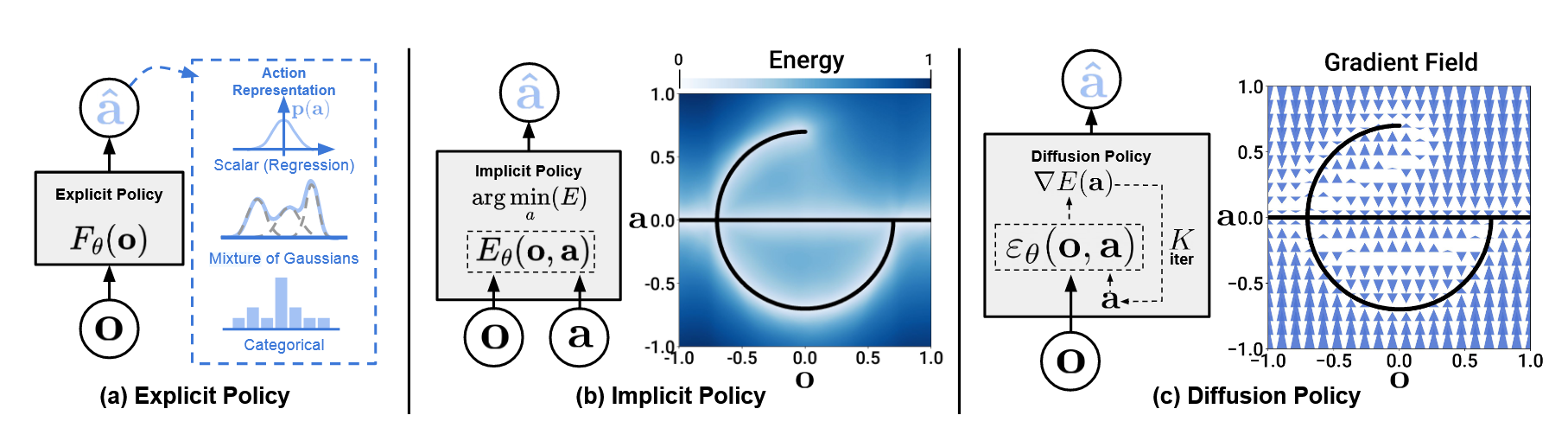
Diffusion Policy

representing a robot’s visuomotor policy as a conditional denoising process.

Diffusion Policy learns the gradient of the action-distribution score function and iteratively optimizes with respect to this gradient field during inference via a series of stochastic Langevin dynamics steps.

优势：

1. 通过学习action score function的梯度，病症这个梯度场上执行 Stochastic Langevin Dynamics sampling, Diffusion policy能够表达任意归一化分布，包括多模态动作分布。

2. 扩散模型已经在图像生成领域的表现，证明了其在高维空间中的可扩展性。这一特性也使得其可以推测一系列的未来行动（而不是单步的），对于action一致性和避免短视规划（myopic planning）非常重要。

3. 基于能量函数的策略通常需要负采样来估计一个难处理的归一化常数。会导致训练不稳定，Diffusion policy通过学习能量函数的梯度来绕过这一问题，来实现稳定的训练并保持distributional expressivity.

Denoising Diffusion Probabilistic Model(DDPM) 去噪扩散概率模型

DDPM

\[x_{k-1} = \alpha(x_k-\gamma\epsilon_\theta(x_k, k)) + \mathcal{N}(0, \sigma^2 I)\]

$\alpha, \sigma$都是noise schedule相关参数。

$\gamma$ 是去噪过程中，沿着”score的负梯度”前进的步长

$\epsilon_\theta(x_k, k)$ 噪声预测网络，预测当前样本中的噪声。其近似$-\nabla_x\log\mathcal{p}(x)$, 即score

其与一次带噪的梯度下降等价

\[x'=x-\gamma\nabla E(x)+\text{noise}\]

$\gamma$控制的是步长，越大，去噪越激进。反之更稳但需要更多step

关于梯度下降

普通梯度下降(Gradient Descent)

假设有一个能量函数$E(x)$

\[x'=x-\gamma\nabla E(x)\]

$\nabla E(x)$是梯度变化最快方向

$\gamma$是步长

带噪梯度下降(Noisy Gradient Descent)

在Diffusion model中，并不是直接使用确定性的梯度下降，而是在每一步上都添加随机噪声。

\[x' = x - \gamma \nabla E(x) + \text{noise}\]

其实这就是所谓的Stochastic Langevin Dynamics.

长时间迭代后，采样结果会分布在目标概率分布$p(x)$上，而非陷入某个点。

DDPM学习的是

而至于为什么要一步一步来，因为DDPM依赖马尔科夫链这一基础假设，这是为什么forward加噪的过程中可以快速处理，而反向只能一步步来。