:construction:施工中-坐标系对齐与透视投影矩阵
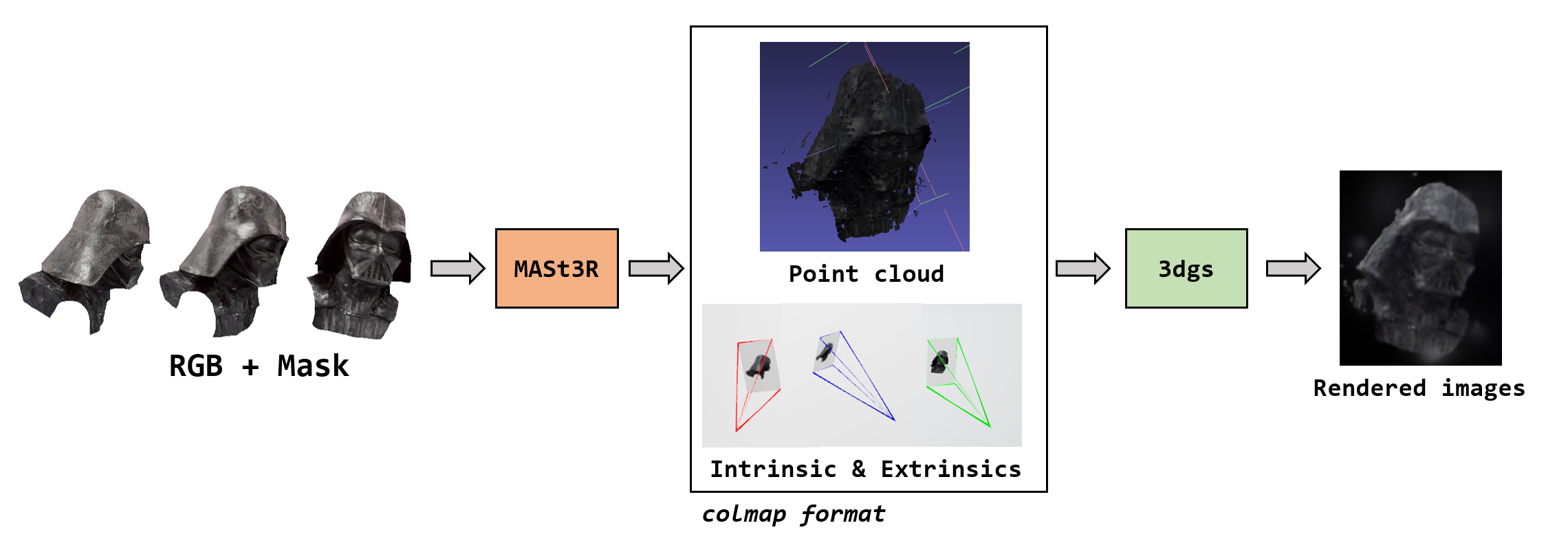
MASt3R + 3dgs
关于colmap format保存数据的部分说明
相机内参保存3×3的$K$矩阵
相机外参保存 4×4的$E$矩阵(world-to-camera), 但是被拆分为$R$和$t$两部分保存, 其中$R$转换为四元数保存
MASt3R会对输入图像进行resize处理, 因此估计的内参和外参绑定的图像尺寸都是resize后的图像尺寸。因此在没有额外处理的情况下,需要保存resize后的RGB和Mask图像(如有需要)
相关issue
https://github.com/naver/mast3r/issues/9
这里提到一个场景:
假设现在有$n$个camera, 分别是$C_0, C_1, C_2, …$, 并且有每个相机相对于世界坐标系的变换$T_{C_{i} \rightarrow W}$。但是由于初始化时的世界坐标系是随机的, 因此要将这些变换都转换到相对于$C_{0}$的坐标变换$T_{C_{i} \rightarrow C_{0}}$
mast3r输出到colmap格式的保存阶段, 保存的相机位姿为w2cam, 即World-to-Camera
colmap的format描述中也是如此要求的。
根据问题:
https://github.com/graphdeco-inria/gaussian-splatting/issues/509#issuecomment-2290932322
关于3dgs中投影的一些讨论:
https://github.com/graphdeco-inria/gaussian-splatting/issues/826
我目前的困惑在于: 我从colmap格式的输出读取的坐标, 在3dgs代码中的渲染结果似乎都存在一个位移上的偏移量, 如下图所示:
绿色点为mast3r中的匹配点的投影结果, RGB图像为mast3r的输出结果输入到3dgs后渲染的图像。
解决方案
这件事情的起因是: 3dgs代码中加载colmap格式的输入时, 相机模型SIMPLE_PINHOLE和PINHOLE都假设相机的光心在图像中心。即cx=width/2, cy=height/2, 而MASt3R估计得到的相机内参$K$在大多数情况下恰恰不满足这个条件,该假设导致了之前提到的渲染结果偏移问题。
1
2
3
4
5
6
7
8
9
10
# https://github.com/graphdeco-inria/gaussian-splatting/blob/54c035f7834b564019656c3e3fcc3646292f727d/scene/dataset_readers.py#L88
if intr.model=="SIMPLE_PINHOLE":
focal_length_x = intr.params[0]
FovY = focal2fov(focal_length_x, height)
FovX = focal2fov(focal_length_x, width)
elif intr.model=="PINHOLE":
focal_length_x = intr.params[0]
focal_length_y = intr.params[1]
FovY = focal2fov(focal_length_y, height)
FovX = focal2fov(focal_length_x, width)
| 3dgs在渲染过程中使用的是FOV视场角投影, 在一般情况下,我们会直接使用$K[R | t]$快速验证MASt3R的投影结果是否正确。绿色点图的结果即$K$投影的结果。 |
3dgs中的投影矩阵计算:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
def getProjectionMatrix(znear, zfar, fovX, fovY):
tanHalfFovY = math.tan((fovY / 2))
tanHalfFovX = math.tan((fovX / 2))
top = tanHalfFovY * znear
bottom = -top
right = tanHalfFovX * znear
left = -right
P = torch.zeros(4, 4)
z_sign = 1.0
P[0, 0] = 2.0 * znear / (right - left)
P[1, 1] = 2.0 * znear / (top - bottom)
P[0, 2] = (right + left) / (right - left)
P[1, 2] = (top + bottom) / (top - bottom)
P[3, 2] = z_sign
P[2, 2] = z_sign * zfar / (zfar - znear)
P[2, 3] = -(zfar * znear) / (zfar - znear)
return P
对应
\[P = \begin{bmatrix} \frac{2 z_{near}}{\text{right} - \text{left}} & 0 & \frac{\text{right} + \text{left}}{\text{right} - \text{left}} & 0 \\ 0 & \frac{2 z_{near}}{\text{top} - \text{bottom}} & \frac{\text{top} + \text{bottom}}{\text{top} - \text{bottom}} & 0 \\ 0 & 0 & \frac{z_{far}}{z_{far} - z_{near}} & -\frac{z_{far} z_{near}}{z_{far} - z_{near}} \\ 0 & 0 & 1 & 0 \end{bmatrix}\]即该计算过程并没有包含$cx, cy$对投影过程的影响。
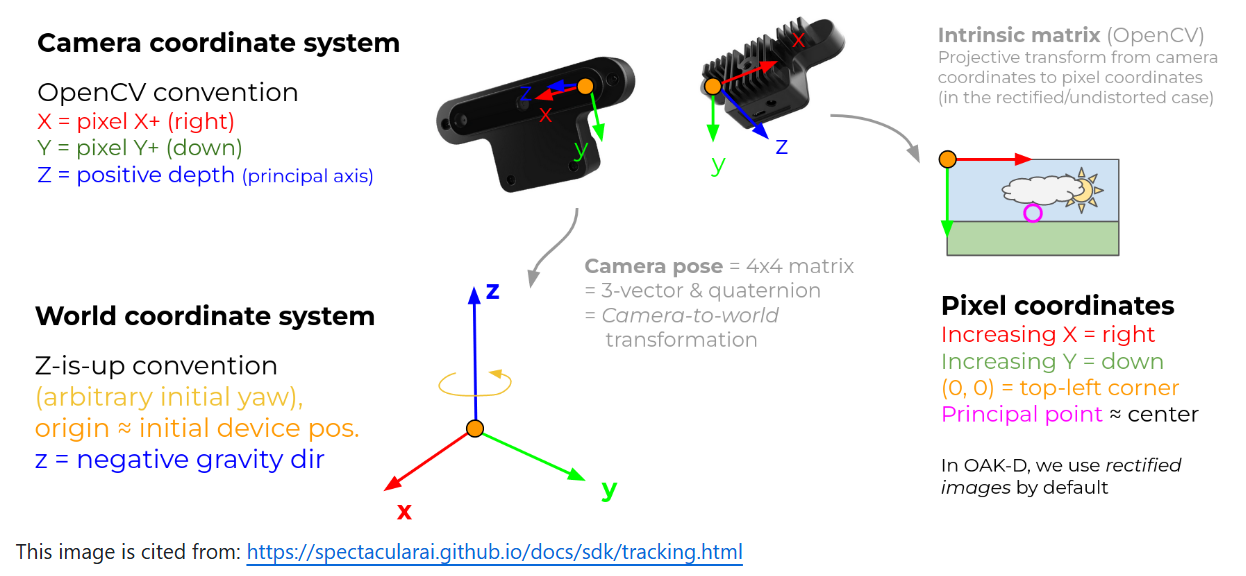
坐标系
关于坐标系
https://github.com/graphdeco-inria/gaussian-splatting/issues/1105#issuecomment-2540601480
关于坐标系和投影矩阵的一部分讨论在这里可以找到
https://github.com/graphdeco-inria/gaussian-splatting/issues/826